ELEC 226, Spring 2010
Prof. Rich Kozick

Laboratory 5
RC Circuits, Time Constants, and an Oscillator

Objective:

In this lab, we will begin with an exercise with RC circuits and time constants. You will learn how to use the oscilloscopes to capture transient events and measure the time constant. Then we will build an “astable multivibrator” or clock circuit using a 741 op amp. The circuit output will be a square wave and a triangle wave, and the frequency of the wave can be adjusted by changing the resistor and capacitor values in the circuit.

RC Circuits and Time Constants:

We will work with the RC circuit in Figure 1. The purpose of the R_s resistor is to prevent a surge of current into the capacitor when the switch is closed. We will use C = 1 micro F and V_s = 12 volts.

Figure 1

Please answer the following questions in your lab notebooks (an outline of the analysis will be given in lab).

1. If the switch has been closed for a long time so that the capacitor is fully charged, what is the voltage v(t) across the capacitor?
2. Suppose that the switch opens at time t = 0 seconds. Analyze the circuit and find an equation describing the voltage v(t).
3. What is the time constant for this circuit, in terms of R_s, R, and C? Make a sketch of v(t), indicating the value of v(t) after 1, 2, 3, 4, and 5 time constants.
4. You should be able to see from your plot where the following two facts and "rules of thumb" about time constants come from:
• The response decays to 36.8% of its original value after one time constant.
• The response has decayed to "zero" after 5 time constants, since the amplitude is less than 1% of the original value.
5. What value of R should be used to obtain a time constant of 1 msec?

Measurements:

Please choose R to achieve a time constant of approximately 1 msec, and choose R_s so that most of the 12 volts appears across the R-C parallel combination when the switch is closed. Consider the case of opening the switch at time t = 0. We will use the oscilloscope to measure the time constant of the circuit. Please set up the circuit in Figure 1 on your breadboard. The lab assistant and I will help you to use the scopes in order to measure the time constant. Record notes in your lab notebook so you can refer to them in the future when you use the scopes. An outline of the procedure that you can use to measure the time constant is as follows. As you know, the scopes are digital instruments, so they can be programmed to perform a lot of useful functions. The steps below allow a single "trace" of the capacitor discharge to be displayed on the oscilloscope. Measurements can then be performed on the trace.

1. Adjust the horizontal (time) axis scaling and the vertical (voltage) scaling to values that are appropriate for the value of V_s and the time constant.
2. Open and close the switch a few times. Make sure the v(t) you observe on the scope matches the sketch you made earlier.
3. Use the MODE key on the scope to set it to record a single trace when you open the switch. Also set the scope to trigger at a level just below v(0), and set the scope to trigger on a negative slope.
4. Use the STOP, RUN, and ERASE keys to record a trace of v(t) after you open the switch.
5. Use the cursors on the oscilloscope screen to measure and compute the time constant. If you use the “%” option in a clever way, then you can get the scope to do all the computations for you in checking the time constant.

Below are some specific activities and measurements to make.

1. Measure the time constant of the circuit using the oscilloscope. Compare the measured value with the expected value based on the R and C component values.
2. Consider the case in which the switch is initially opened and then closed to charge the capacitor. Use the oscilloscope to capture one trace of the charging capacitor. Note that the procedure needs to be modified slightly to capture this trace.
3. Modify the circuit to achieve a time constant on the order of one second. Use the oscilloscope to verify that the time constant is indeed about one second.
4. Try to analyze the circuit for v(t) when the switch is closed to charge the capacitor. What is the time constant in terms of R_s, R, and C?

Op Amp Clock Circuit:

Look at the circuits in (a) and (b) of Figure 2. How will each circuit operate? Which one will oscillate? How is the period (or frequency) of oscillation related to the R and C values? Please note that the circuits may not be connected with negative feedback, so consider whether the op amps are saturated.

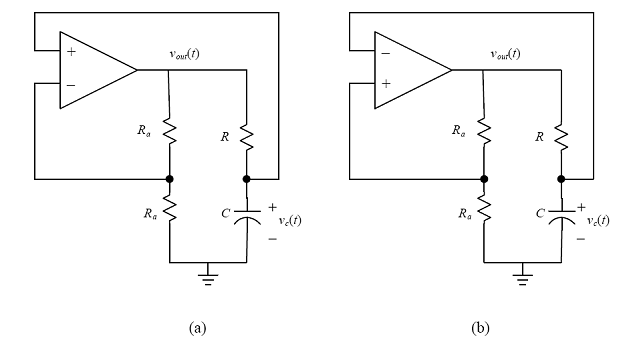
Figure 2

Perform the following activities.

1. Please make a rough sketch (on a single plot) the capacitor voltage v_c(t) and the op amp output voltage v_out(t) versus time for the oscillator circuit. How is the period of the wave related to the values of R and C (an exact equation is not needed today)?
2. What value should you choose for the resistor R_a? Why? If R is a potentiometer that varies from 0 ohms to 100 k ohms, what value of C should you use to produce a clock frequency as low as 1,000 hertz? How can you modify the circuit to produce clock frequencies in the range from 100 to 1,000 hertz?
3. Set up and test your circuit. Demonstrate how the frequency of your clock circuit varies as you change the potentiometer. Observe both v_c(t) and v_out(t) on the oscilloscope.
4. What if the pair of resistors with value R_a are replaced by resistors with values that are not identical? Can you make a triangle wave generation circuit? Try it!!

If you finish the previous activities, you may apply the integrator and differentiator circuits from Lab 4 to the square wave and triangle wave produced by your clock circuit.

No report is needed for this lab, but keep your clock circuit assembled for use in the next labs.